The R-Score
The R-Score, officially the cote de rendement au collégial (CRC), is a number or score you receive for each course you take in CEGEP. It's used for university admissions in Quebec to assess your academic performance. An overall R-Score is also calculated, which is the weighted average of all individual R-Scores from each of your courses—the number of credits a course is worth determines the weight of each course when calculating the overall R-Score. The Bureau de coopération interuniversitaire (BCI) is responsible for calculating R-Scores.
Why does the R-Score exist? According to the BCI, two correction factors are used in the R-Score formula so that not only the student's own academic performance in a course is taken into account, but also the group strength and dispersion (academic strength and performance of your classmates). This adjustment is particularly important when it comes to Quebec university admissions, since applicants attend various CEGEPs across the province, forcing universities to compare students who were evaluated based on different college grading systems. In a nutshell, the R-Score was devised as a way to rank students more fairly.
Now, on to the math! The concept of the R-Score and its formula can be confusing, but in the end, it really boils down to basic statistics. To know how the R-Score works, you'll first want to understand standard deviation and z-scores.
First, here's some vocabulary you should know:
- Deviation = how far from normal, from a norm, something is
- Data set = a collection of related values/data points (often numbers)
- Data point = an element (usually a number) in a data set
- Distribution = in statistics, distribution is the way in which something (usually data) is "spread out" or distributed
- Bias = in statistics, bias indicates that data is skewed, or more spread out, in a certain direction (left/right)
- Left-skewed= more spread out on the left
- Right-skewed= more spread out on the right
Left-skewed data example
Graph from Mathisfun. Copyright by MathsIsFun, 2019.
- Normal distribution = data that is distributed evenly around a central value, with no bias left to right. Data is considered normal or normally distributed when:
- Mean = median = mode
- It's vertically symmetrical (50% of values less than the mean and 50% greater)
- A common example of normal distribution is called the Bell Curve:
Bell Curve diagram
Diagram from Mathisfun. Copyright by MathsIsFun, 2019.
- Mean = the average, calculated by taking the sum of all numbers and dividing that sum by the quantity of data points
- To find the mean of 2, 3, 5, 10, we take the sum: 2 + 3 + 5 + 10 = 20, then divide that sum by the quantity of data points (here, we have 4 numbers/data points): 20 / 4 = 5
- Population = in statistics, a population is a collection of items (ie. a pool of individuals) under consideration, from which statistical samples may be drawn for a study
You can also read Marianopolis College's document on the R-Score, the main information source for this page, here: March 2018, New R-Score Formula
Standard Deviation
Standard deviation is the measure of how spread out numbers are, and is represented by the symbol σ (lowercase Greek letter sigma). It gives us a way of knowing "what's normal". Now, the formula for standard deviation involves something called the variance, which we'll go ahead and define next.
The definition of variance is the average of squared differences from the mean. There are three steps to calculating the variance:
- Calculate the mean of the data set.
- For each data point: subtract the mean from the number (even if the result is negative!), then square the result.
- Calculate the average of all squared differences (from step 2).
Here's an example with some people's heights:
For heights (standing, from head to toe) 157 cm, 160 cm, 172 cm, 165 cm and 181 cm, calculate the variance.
- Calculate the data set mean: 157 + 160 + 172 + 165 + 181 = 835, there are five data points so 835 / 5 = 167
- Calculate the squared mean differences:
- Subtract the mean from the number for each data point: 157 - 167 = -10, 160 - 167 = -7, 172 - 167 = 5, 165 - 167 = -2, 181 - 167 = 14
- Square each mean difference: (-10)2 = 100, (-7)2 = 49, (5)2 = 25, (-2)2 = 4, (14)2 = 196
- Calculate the average of all squared differences: 100 + 49 + 25 + 4 + 196 = 374, there are five data points so 374 / 5 = 74.8
∴ We can conclude that the variance of these heights is 74.8.
Now, to go from the variance to standard deviation is extremely simple. The definition of and formula for standard deviation is just the square root of the variance.
Let's calculate the standard deviation for the same data set:
- Calculate the square root of the variance: √74.8 = 8.648699324 ≈ 8.6
∴ The standard deviation of the heights is (approximately) 8.6 cm.
As mentioned earlier, standard deviation provides us with a standard whereby we can identify what's normal, and what values are further away from that standard (smaller, larger, etc.)—but how does the calculated value translate to this?
Since variance and standard deviation are calculated based on the mean, the "normal" data points are determined in relation to the data set's mean. We can consider the mean to be the "most normal value", then using the standard deviation, we can find the range of normal values. So you can almost think of standard deviation as a unit, designated by σ: in a normal distribution like the Bell Curve, values within 1 standard deviation of the mean are considered normal.
Let's find the "normal range" for our set of heights, where the mean is 167 and the standard deviation is 8.6:
Any value within one standard deviation is normal, so we want to find a range where values that are one standard deviation less than the mean are included, as well as values that are one standard deviation greater than the mean.
- The lower bound/minimum value: 167 - 8.6 = 158.4
- The upper bound/maximum value: 167 + 8.6 = 175.6
∴ We can conclude that for this data set, any value within the range of 158.4 - 175.6 (that is, heights from 158.4 cm to 175.6 cm) is considered to be normal.
In statistics, about 68% of values in a normally distributed data set can be expected to be within plus-or-minus one standard deviation (± 1σ), or within the "normal range". As shown in the diagram below, we expect about 95% of values to be within plus-or-minus two standard deviations (± 2σ), then that percentage becomes 99.7% within plus-or-minus-three standard deviations (± 3σ).
This is what we call the Empirical Rule, or the 68-95-99.7 rule (or even the 95 rule, as 95% is very commonly used as an interval).
Recall that lowercase sigma σ is the symbol for standard deviation.
Standard deviation diagram
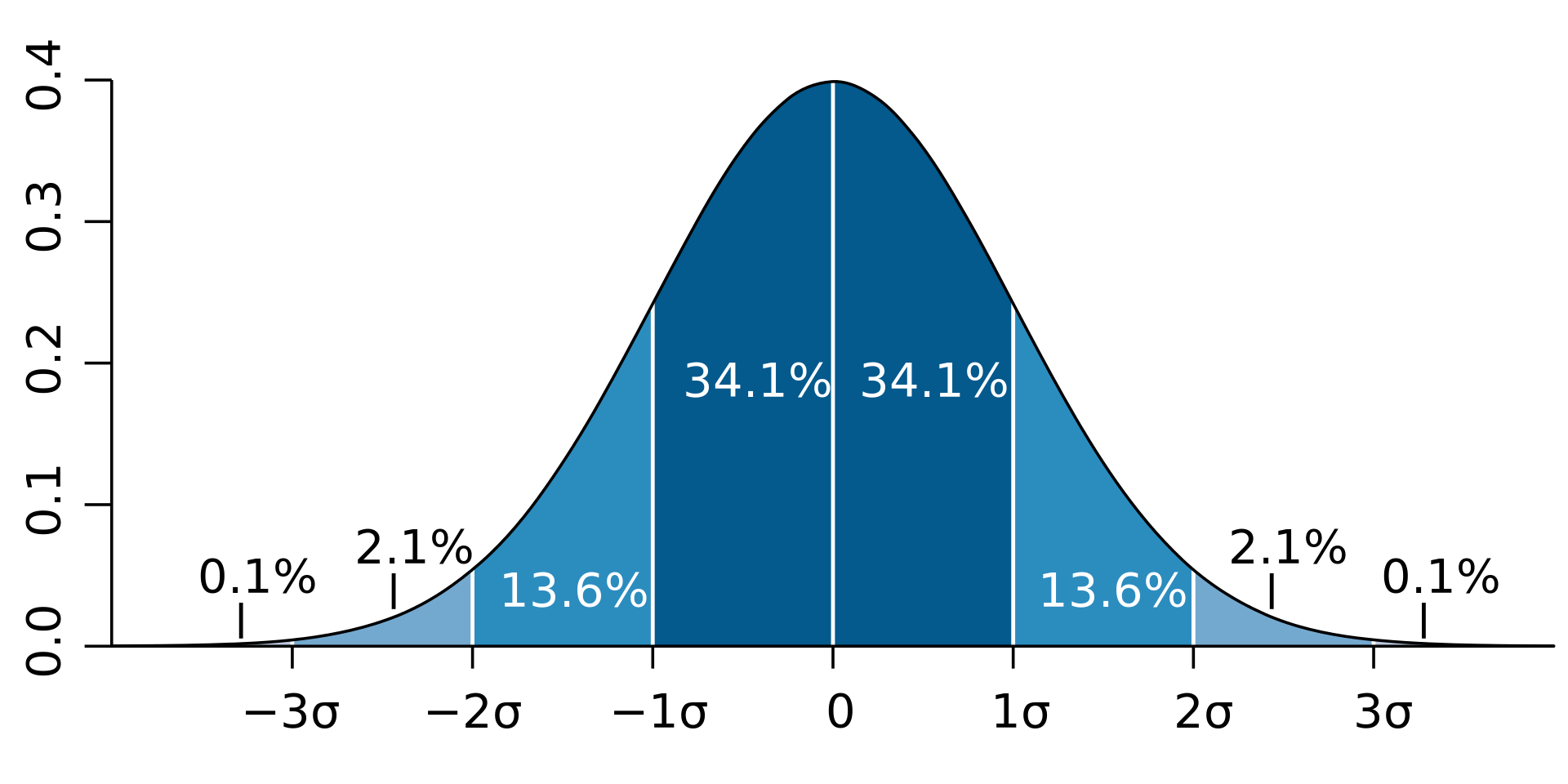
Diagram by M. W. Toews, CC BY 2.5 licence
Just one final detail before we move on: the calculations shown above are used for a population, meaning the data points we used were the only ones we were interested in. (We got heights from five people, and we only cared about the heights of those five people.)
There's a small change when calculating variance and/or standard deviation for what's called a sample, a selection taken from a larger population. (We got heights from five people, and maybe we're using that data to represent a group of fifteen people or more.) However, since R-Score calculations likely use population data (data from all students concerned), we'll just focus on the calculations that were already presented and explained.
If you want to read about calculating variance and/or standard deviation for a sample, check out this lesson on Mathisfun: Standard Deviation and Variance
Mathisfun — Standard Deviation, Mathisfun — Normal Distribution, Penn State University — The Empirical Rule
The Z-Score
A z-score measures, for a data point, how many standard deviations above or below the mean it is. Z-scores are also called standard scores in statistics.
The formula for calculating a z-score is quite simple: you divide a data point's mean difference by the data set's standard deviation. It could be written like this: (data point - mean) / standard deviation = z-score
Some key facts on z-scores:
- If a data point has a positive z-score (greater than 0), it's above average (above the mean)
- If a data point has a negative z-score (less than 0), it's below average (below the mean)
- If a z-score is close to 0, the data point is close to average (close to/approaching the mean)
- Depending on the context, the general guideline is that z-scores above 3 or below -3 are considered unusual
- Different people may use different ranges, such as ±2 or ±2.5
- In R-Score calculations, we'll see later on that the BCI uses two different cutoffs pertaining to z-score components
Why is it 3 and -3? Let's think back to the empirical rule with this diagram here:
Empirical rule histogram
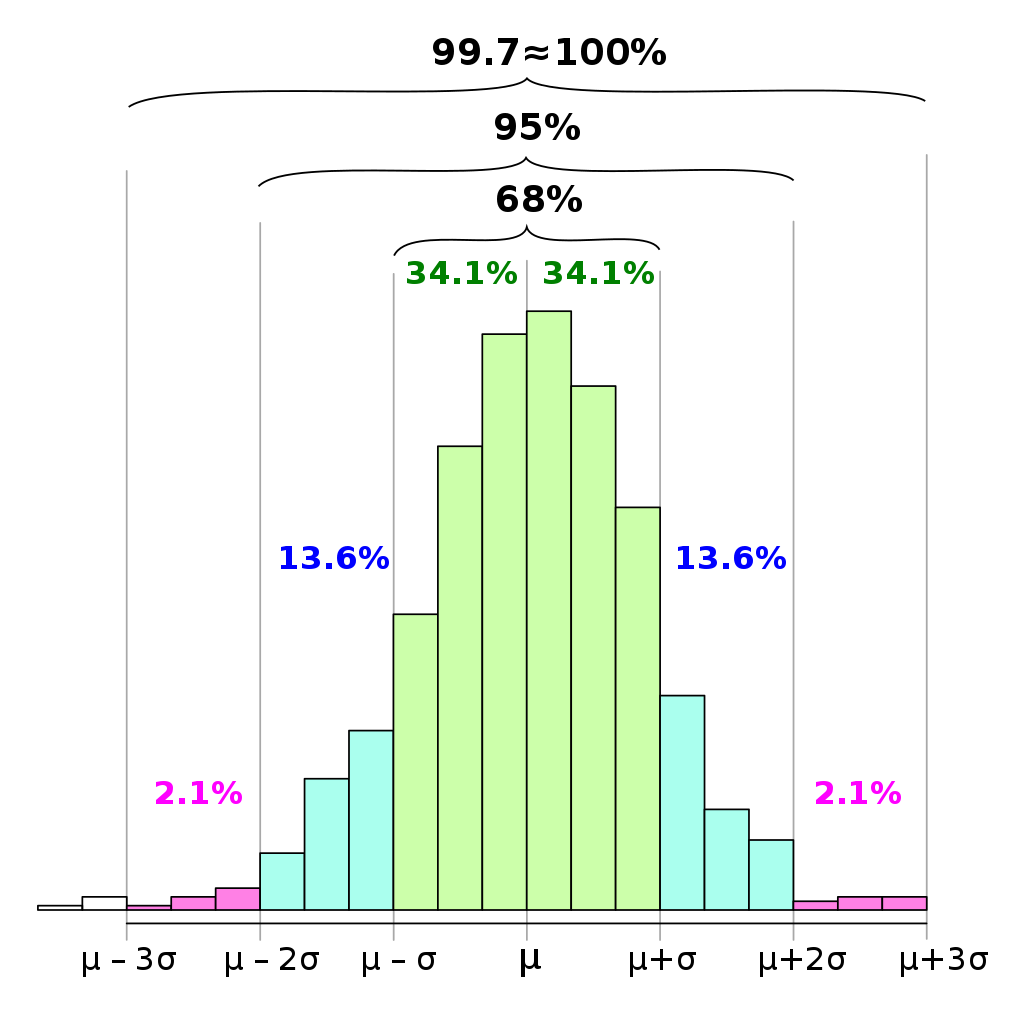
Diagram by Melikamp, CC BY-SA 4.0 licence
The symbol μ is lowercase Greek letter "mu", which is statistical notation for the mean. Recall that a z-score is defined as how many standard deviations above or below the mean a data point is.
Notice and recall that between plus-or-minus-three standard deviations (± 3σ), around 99.7% of values in a normal data set can be expected to fall within that range. To rephrase, we can expect around 99.7% of values in a normally distributed data set to fall within three standard deviations of the mean.
So, if we think about this in terms of the z-score, this means that data points with a z-score between 3 and -3 fall within the three standard deviation range—a z-score of 3 means a data point is 3 standard deviations above the mean, and a z-score of -3 means a data point is 3 standard deviations below the mean. To put it simply, data points with a z-score between 3 and -3 represent those 99.7% of values mentioned earlier.
We can thus conclude that it would be extremely rare and unusual for a data point to fall outside of this range (± 3σ, or for z-scores, between 3 and -3), where we expect a mere 0.3% of values to be.
Let's practise calculating z-scores with a couple of random examples:
- The grades on a French midterm at Eastwood High have a mean of 85 and a standard deviation of 4. If George scored 86 on
the exam, what is the z-score for his exam grade?
First, considering the z-score formula, (data point - mean) / standard deviation, we see that data point = George's exam grade = 86, mean = 85, and standard deviation = 4. Let's substitute those values in:
z = (data point - mean) / standard deviation
z = (86 - 85) / 4
z = 1 / 4 = 0.25
∴ George's z-score is 0.25, meaning his grade is a quarter of a standard deviation above the mean.
- The grades on a history midterm at Eastwood High have a mean of 83 and a standard deviation of 2. George scored 79 on
the exam. What is his z-score for the history midterm?
Data point = George's exam grade = 79, mean = 83, standard deviation = 2. Let's substitute these into the formula:
z = (data point - mean) / standard deviation
z = (79 - 83) / 2
z = (-4) / 2 = -2
∴ George's z-score is -2, meaning his grade is a half of a standard deviation below the mean.
Want to practise calculating z-scores? Check out this Khan Academy exercise: Calculating z-scores
Sources: Z-scores — Khan Academy
Understanding the R-Score Formula
Since March 2018, the BCI has used the following formula to calculate an R-Score in a single course (recall that R-Scores are calculated for each of your college courses):
Rcourse = (Z ⋅ IDGZ + IFGZ + 5) ⋅ 5
Let's go over each component:
- Z = your z-score for the course
- (your course grade - the course mean) / the course standard deviation
- Notice that here, your course grade = the data point (in the z-score formula)
- IFGZ = l'indicateur de la force du groupe (the third component: we'll go over this first so that the IDGZ makes more sense)
- This component measures the so-called strength of the group
- Students in the course are given high school z-scores, which are z-scores based on their academic performance in certain standardized (ministerial) high school courses
- The IFGZ is the average of these high school z-scores (the mean): (sum of student high school z-scores) / (number of z-scores)
- The IFGZ is capped between -2 and 2
- IDGZ = l'indicateur de la dispersion du groupe (the second component)
- This measures the dispersion of the high school z-scores of you and your classmates for a course. In other words, the IDGZ is the standard deviation of high school z-scores of students part of the same course.
- The square root of the variance of high school z-scores
- Values of the IDGZ are capped between 0.5 and 1.5
Here's a look at how the IDGZ may be calculated:
- Find the high school z-score mean, or the mean of all high school z-scores of students in the course.
- For each student's z-score, find the mean difference: subtract the mean from the student z-score (student z-score - z-score mean)
- Calculate the average of all squared differences from the previous step:
- Square every mean difference: (student z-score - z-score mean)2
- Add them all together, then divide that sum by the number of student z-scores used for the IDGZ. (Recall that only IDGZ values between 0.5 and 1.5 are used later to calculate R-Scores.)
- The two 5s (+ 5 and ⋅ 5) = "aesthetic" factors/components
- The plus 5 and times 5 in the formula are essentially for "aesthetic purposes". They shift and scale the R-Score into a "nicer range", which is around 0-50.
Sources: Marianopolis College — New R-Score Formula, BCI — The R-Score
Summary, Analysis, and Takeaways
Now that we understand how the R-Score is calculated, how does it work and what does it actually do? Let's take another look at the formula, specifically the IDGZ component:
Rcourse = (Z ⋅ IDGZ + IFGZ + 5) ⋅ 5
- The IDGZ (group dispersion) multiplies the college course z-score
- The formula adjusts, depending on the IDGZ value, the weight of:
- Your performance in the course (Z)
- The group strength (IFGZ)
For simplicity, let's disregard the two aesthetic 5s:
Rcourse = (Z ⋅ IDGZ + IFGZ)
- If the IDGZ < 1, the value of (Z ⋅ IDGZ) decreases. Therefore, the weight/importance of your performance in the course is diminished relative to the group strength (IFGZ).
- What does it mean if the IDGZ < 1? Since the IDGZ is the course group's z-score standard deviation and is limited to a range of 0.5 to 1.5, IDGZ < 1 means that there's less spread/distribution in your course group.
- Less spread = the high school z-scores of your course group are all quite similar/close to each other and have a smaller range (the difference between the highest and lowest z-scores is smaller)
- (Lower standard deviation = a set of data points are more closely grouped, are closer in value)
- If the IDGZ > 1, the value of (Z ⋅ IDGZ) increases. Therefore, the weight/importance of your performance in the course
is amplified (increased) relative to the group strength (IFGZ).
- What does it mean if the IDGZ > 1? A higher standard deviation means that the data points in a data set are more spread out, and since the IDGZ is the group's dispersion/standard deviation, a higher IDGZ (> 1) means that there's more spread in your course group.
- More spread = the high school z-scores of your course group vary quite a bit have a wider range (the difference between the highest and lowest z-scores of the group is larger)
- Because the IDGZ is capped between 0.5 and 1.5, your performance in a course will always remain an important factor in R-Score calculation.
To summarize these points:
- If the high school z-scores of a course group are less spread out, the importance of your own performance in the course
is diminished.
- The weight of the group strength thus amplifies
- If the high school z-scores of a course group are more spread out, the importance of your own performance in the course
is amplified.
- The weight of the group strength thus diminishes
- In both cases, your own course results are an important factor!
- In both cases, students may benefit from a strong course group ("high" group strength, which translates mathematically as a larger IFGZ value)
Now, let's go over how and where the R-Score is used, as well as some useful facts:
- Individual R-Scores are calculated for each CEGEP course.
- Provided at least six students in the course group achieve a percentage grade of 50% or above (if you do not receive an R-Score for a course, this condition was likely not met)
- An overall R-Score is calculated as the weighted average of all course R-Scores (the weight of each R-Score depends on
the number of credits the course is worth).
- Failed courses count for less in your overall R-Score; that is, they are given less weight in the calculation of your overall R-Score.
- R-Scores usually fall between 15 and 40.
- A high R-Score is typically said to be 30 and above.
- Extremely competitive programs such as Law, Medicine, and Dentistry generally require an R-Score in this range
- When calculating the IFGZ (average of high school z-scores), the following secondary school courses are taken into
account:
- Secondary 4 History
- Secondary 4 Science
- Secondary 4 Math
- Secondary 5 Language of Instruction (English/Français)
- Secondary 5 Second Language (Français/English)
The R-Score is used by Quebec universities for admissions purposes in addition to other criteria (admission essay, CV, interview, etc.). R-Score cutoffs are often set for programs, and these cutoffs can be found on university websites (note that cutoffs may vary from year to year!). Here are some examples for 2023:
- McGill Finance: 28.30-29.6 overall, 28.3-30.0 core math/science, 26.0 English
- Concordia Art History: 19
- Concordia Computer Science: 28 overall, 26 math
- McGill Electrical Engineering: 29.8 overall, 29.8-30.0 math/science
Sources: McGill University, Concordia University
The R-Score is not the only admission criteria for university, and it is only considered by Quebec universities.
There are formulas with official statistics notation that weren't shown here for simplicity. The formulas are really just the fancy and standard way of representing the concepts and calculations explained on this page. You can learn about them here: Standard Deviation Formulas
References
Here are the main R-Score documents referenced in this page.
Marianopolis College's document on the newer R-Score formula: March 2018, New R-Score Formula
BCI (Bureau de coopération interuniversitaire), an FAQ on the R-Score from September 2020: R-Score Questions and Answers
In section 2 of the following document, you can find some tables demonstrating how students may be ranked differently using percentage grades, z-scores, and R-Scores: The R-Score: What it is and What it Does
To learn more about the R-Score (all documents) from BCI, the body responsible for its calculation, visit their site: https://www.bci-qc.ca/en/therscore/
Want to find out how to apply to CEGEP, or get some tips on choosing a college and program?
Looking to visit the official CEGEP sites, or looking for viewbooks, handbooks, and more?
Not sure where to go next?
Think CEGEP might not be for you? Continue to Alternatives to CEGEP.